Beams
전단력만의 변형
- 하중은 고정된 지점에서 보를 전단하려는 경향이 있습니다.
- 전단경향은 보의 전체에서 발생합니다.
- 캔틸레버보의 경우 하중이 내민 끝에 작용할 경우 전단 경향은 보 전체에서 동일합니다.
- 캔틸레버보의 경우 하중이 보 전체에 균일하게 분포될 경우 전단하려는 경향은 고정단에 가까울수록 전단력이 크게 분포합니다.

등분포 하중이 작용하는 캔틸레버보의 전단력 분포
- 보의 수직전단력 발생의 예
- 여러권의 책을 양쪽 손으로 받치고 있다면 책이 자체의 무게 때문에 서로 미끄러지려는 경향을 나타냅니다.
- 이러한 경향을 이겨내고 책을 들어올리려면 양쪽에서 큰 힘으로 눌러 미끄러지지 않게 큰 마찰을 발생하여야 합니다.

전단- 직각되는 두면에서 미끄러짐이 발생
- 구성요소를 돌리려는 경향
- 회전 이동이 발생 - 회전 이동을 방지하기 위해 수평면에서 반대방향의 힘 작용
- 수직에 의한 전단력은 수평전단력을 향상 수반한다.
- 서로직교하는 인장과 압축의 합성으로 여길 수 있다.
- 수평전단력을 나타내는 수평으로 여러겹으로 나누었을 경우의 처짐
- 보를 일정한 두께로 나누어 생각해보자 여러겹으로 나누어진 보는 하나로 된 단일 보다 처짐이 크다.
- 여러토막들의 미끄러짐은 보의 파이버들이 수평면을 따라 전단하려는 경향이 있다.
- 즉 수평으로 전단하려는 경향을 나타낸다. - 전단응력으로 저항이 가능하다.
- 전단 응력을 가하는 방법으로는 나누어진 토막의 접착, 수픽 핀으로 고정, (a),(b)의 단면이차모멘트의 차이 1:1/16으로 보의 처짐이 (b)가 16배가 된다.
I형보에서 웨브의 기능
- 상하의 두플랜지가 함께 작용하는데 필요한 전단응력을 일으킨다.
- 웨브가 없다면 분리된 엷은 보로 작용 단면 2차 모멘트가 작아진다.
- 웨브를 통한 상하의 플랜지로의 전단의 전달은 플랜지의 휨작용에 필수적이다.
- 전단과 휨은 서로 의존하는 보의 작용입니다.

전단응력의 분포
- 중립축에서 최대인 포물선 분포
단순지지보
- 보 단부(양단)의 회전이 자유롭고 보의 신축이 축방향으로 자유롭게 보를 양단에서 지지하였을 경우의 보
- 중앙부에 가한 하중의 반씩을 지지점으로 전달
- 좌우대칭으로 중앙을 잘라서 보면 거꾸로 된 켄틸레버 보와 같은 작용이다.

단순지지보 상의 집중하중

- 단순지지보와 켄틸레버 보의 처짐 비교
- 켄틸레버 보의 처짐은 하중과 보길이의 세제곱에 비례 - 나누어진 두개의 캔틸레버의 경우 하중이 1/2, 길이가 1/2이다. , 캔틸레러보의 처짐의 1/8의 반 즉 1/16배가 된다.
- 단순지지보는 같은 길이의 켄틸레버보 보다 강하고 강성이 크다. - 4배의 하중지지, 처짐이 1/4이다.
- 등분포하중을 받는 단순지지보 - 휨응력은 중앙에서 최대, -전당응력은 중앙에서 zero
- 휨응력이 가장 최대인 지점에서 전단작용이 zero가 된다. - 모든 보의 특성
하중위치에 따른 전단하중의 분포
- 모든 지점에서 전단과 휨의 작용을 받는다.
- 하중이 지지점에 가까울수록 전단작용이 크다.
- 하중이 지지점 바로 옆에 있을 경우 전단력은 전체하중과 동일하다.
- 하중이 중앙에 있을 경우 전단력은 하중의 반이다.

전단
- 인장과 압축의 결합
- 지지점 가까이에서 최대전단
전단보강하지 않은 철근 콘크리트 보
- 지지점 가까이에서 45의 경사균열 발생
- 전단보강 방법 - 수직 혹은 경사근 보강
철골보의 전단보강
- 물결모양의 좌골을 방지하기 위해 수직스티프너로 보강
단면형태
- 캔틸레버보와 같다.
- 단면적, 사용재료의 양에 비례한다.
- 재료가 중립측에 떨어져 있는 회전반경이라는 거리의 제곱에 비례한다.
- 보의 처짐과 휨응력 : 단면 2차 모멘트에 반비례
큰보의 경우에는
- 변단면을 사용한다.
- 중앙부의 춤을 높이는 방식대신 플랜지의 면적을 늘린다.
하중의 방향에 따른 상하단의 응력
-하향하중
- 상부에 압축 / 하부에 인장
-상향하중 (예:지중보)
- 상부에 인장
- 하부에 압축
보의 중립축 근처
- 중립축에서는 인장, 압축력이 zero
- 구멍을 뚫어 일부를 제거하여 보를 경량화한다.
- 구멍이 점점 커짐에 따라 - 트러스가 됩니다.
- 트러스를 구멍 뚫린 보로 본다면? - 상현재, 하현재 - I형보의 플랜지 역할 - 사재, 수직재 : 전단력을 흡수하는 불연속 웨브역할

마리카이보 교
- 긴거리를 걸치는 철근 콘크리트 교량
- 캔틸레버로 고정된 부분과 단순지지된 중간보들들로 구성
단순지지보의 특성
단순지지보의 특성
- 휨응력에 의한 인장, 압축이 중앙에서 최대치 도달 - 재료사용에 비능률적 구조
- 전체적으로 아래로 볼록한 변형곡선, 중앙에서 최대곡률(처짐) 및 최대 모멘트
지지점의 안쪽으로의 이동
- 보의 효율을 증대
- 두개의 캔틸레버 구조
- 곡률 반대, 단부는 아래쪽으로 처짐
단순지지보와 고정단 보의 비교
- 고정보 : 보의 양단의 회전변형이 구속
- 1:2.5의 길이비를 갖는 보와 같은 성질
- 고정단에서 최대응력 발생, 중앙부응력의 2배, 단순지지보의 최대응력의 3/2
- 단순지지보 보다 50% 많은 하중을 받을 수 있다.
- 단순지지보다 5배의 강성, 처짐이 1/5
- 고정단 철근 콘크리트 보의 인장(철근)보강 위치- 중앙부 하단, 지지점 상단
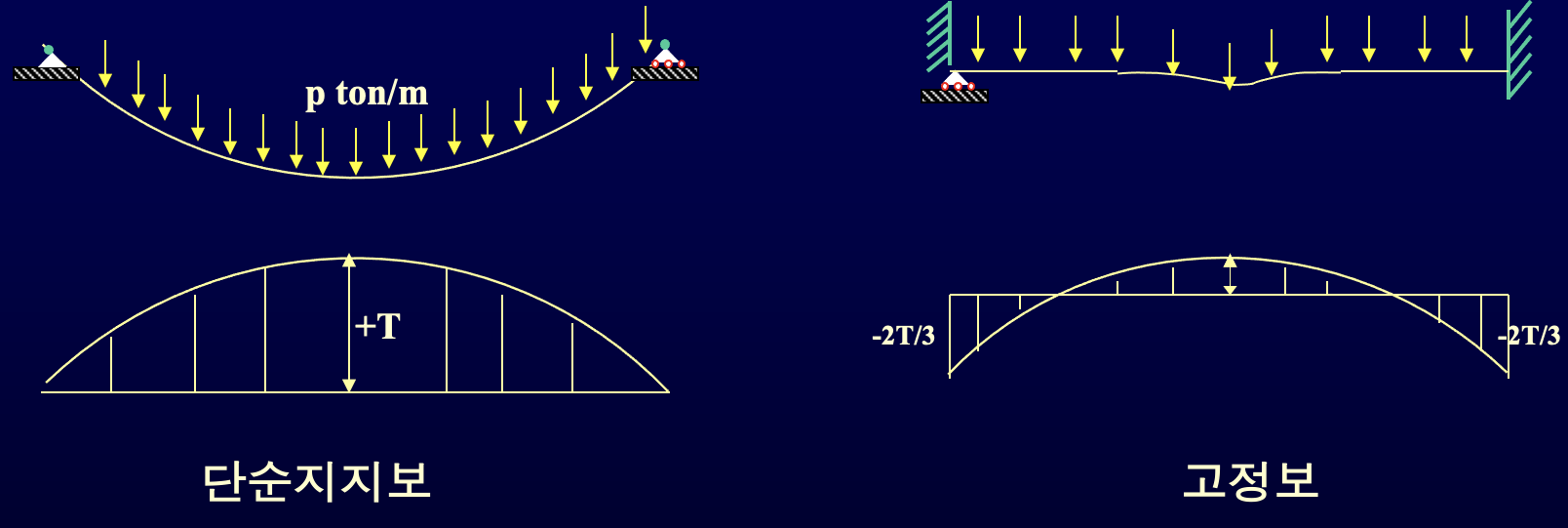
고정보
- 처짐 : 두반곡점에서 처짐곡률이 변화
- 반곡점 휨응력 zero, 응력의 부호가 바뀜
- 휨응력이 없다 - 두점에서 단순지지된 것과 같은 작용
- 단순지지보 보다 50% 많은 하중을 받을 수 있다.
고정보를 달리 생각하면
- 고정단 양쪽에서는 고정된 캔틸래버보
- 중앙부에서는 짧은 거리를 단순지지한 보의 합성보다 큰 하중지지 능력과 강성이 있다.
2차 휨응력
- 적응력 : 구조부재 단면에서 늘 일정한 압축응력과 인장응력
- 재료의 효과적인 사용이 가능하다.
- 트러스부재 : 단순인장, 단순압축만 작용 - 부재단면의 모든 지점에서 최대저항력 발휘
- 직응력의 특성 - 휨변위에 대해 극히 작은 변위를 나타낸다.
- 자의 압축 및 휨에 의한 변위
- 압축력에 의한 처점은 육안으로 감지하기 어렵다.
- 휨처짐은 쉽게 볼 수가 있다.
구조물의 특성
- 휨에서보다 압축 혹은 인장에서 더욱 강하다.
- 휨처짐은 같은 하중에 의한 압축변위보다 2000에서 3000배정도가 크다.
- 순전한 압축, 혹은 인장만 받을 수 있는 구조부재는 거의 없다.
- 예를 들어 단순 트러스만 해도 작지만 어느 정도의 휨을 받기도 한다.
2차 휨 응력
까치발 트러스
- 사재 : 인장 수평재: 압축작용으로 하중 지지
- 단부의 회전이 자유로울떄만 직응력 (순수 축하중이 발생)
- 수평재의 단부가 고정된 경우 : 하중의 일부를 휨작용으로 지지
- 회전에 대해 구속되지 않은 회전이 자유로운 접합 :힌지접합(hinge)
모든 트러스가 단슨한 직응력 즉 순수 축하중만 작용하게 하기 위해서는 모든 접합이 힌지접합이어야 한다.
- 과거에 존재
- 비바람에 의한 부식에 의한 접합부의 힌지역할 상실의 경우가 많아 최근 트러스부재는 경제성을 위해 볼트 혹은 용접을 한 접합부를 사용한다.
힌지접합과 용접접합의 비교
- 힌지접합 - 두부재의 접합부에서 회전이 발생, 길어진 부재는 길어진채로 축소된 부재는 축소된 채로 회전되어 처음의 두 부재간의 각도가 변한다.
- 용접, 리벳이나 볼트 접합 - 두부재의 접합부에서 회전이 구속되므로 각도는 변화하지 않는 대신 부재가 휘게 된다.
728x90
그리드형
'건축' 카테고리의 다른 글
| 건축에서 빛의 성질 - 빛의 개념과 장단점 (0) | 2022.03.24 |
|---|---|
| 광주 HDC아파트 붕괴사고 주요 원인 "무단 구조변경"- 콘크리트 품질관리, 감리 소홀 등 전반적 관리 부실로 인한 붕괴. (0) | 2022.03.23 |
| 아일랜드 더블린 발리문 도시재생 연쇄형 지역재생사업 (0) | 2022.03.17 |
| 건축과 환경 - 친환경 건축(기후, 건축내부환경,환경조절방법,환경친화건축) (0) | 2022.03.14 |
| 건축 콘크리트 프리텐션과 포스트텐션 차이점 (0) | 2022.03.13 |





댓글